Práctica: Método de Newton - Raphson

Algo que no mencioné en la entrada anterior de la definición de este método es que al encontrar los ceros de su primera derivada podemos encontrar el máximo o mínimo de una función.

En este caso, nuestra práctica aborda la característica principal encontrar las aproximaciones de los ceros o las raíces de una función real.

Aquí esta presentado el código usado, es importante mencionar que ahora involucramos directamente la derivada de la función en juego. 

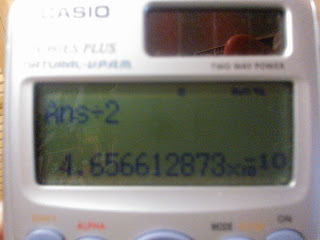
Seguimos usando f(x) = cos (x), la máquina nos arroja un valor determinado de cifras significativas, los cuales consideraremos como si lo fuese en calculadora, ahora bien si se va siguiendo con un calculo a mano, podremos usar el redondeo truncado como lo dijimos en las entradas anteriores.

Resultados en pantalla:

Como podemos observar la principal diferencia con respecto a los métodos anteriores es que Newton - Raphson, no trabaja con intervalos donde nos asegure que encontraremos la raíz, y de hecho no tenemos ninguna garantía de que nos aproximaremos a dicha raíz. Desde luego, existen ejemplos donde este método no converge a la raíz, en cuyo caso se dice que el método diverge. Sin embargo, en los casos donde si converge a la raíz lo hace con una rapidez impresionante, por lo cual es uno de los métodos preferidos por excelencia.

Método de Newton - Raphson

Es también conocido simplemente como método de Newton y es otro método de iteraciones para resolver ecuaciones f(x) = 0, donde f es diferenciable. La idea es la de construir una aproximación a la gráfica de f mediante tangentes apropiadas. Usando un valor Xo obtenido de la gráfica de f, sea x1 el punto de intersección del eje x y la tangente a la curva de f en Xo.

Entonces: 

De donde:

Y así de manera sucesiva, de tal forma que la ecuación general del método de Newton – Raphson es:

Práctica: Método de Aproximaciones Sucesivas

Retomemos la definición y recordemos que el método de Aproximaciones sucesivas consiste en encontrar una raíz de una ecuación algebraica mediante la modificación de la misma y realizando un determinado número de iteraciones que indiquen que el sistema tiende a converger.

La ecuación que usamos es:

 f(x) =  x - cos (x)

o bien:

x = cos (x)

Aquí esta el código usado, donde al igual que en la práctica anterior usamos un ciclo (for) para repetir n numero de veces el algoritmo.

Resultados:

con 3 iteraciones:

Como conclusión es importante recalcar que en este método para los resultados que registramos en la libreta y en la evaluación por parte del profesor utilizamos en redondeo simétrico y truncado por facilidad, sin embargo así como hemos venido viendo el error aumenta como tal, aún así dependerá de los factores de precisión en nuestra calculadora.

Método de Aproximaciones sucesivas

Supóngase la siguiente ecuación:

x = F(x)

Generalmente esto se puede hacer de muy diversas maneras. Por ejemplo, si.

En donde c ³ 0, podemos sumar x en ambos miembros para obtener

Como un último ejemplo, podemos re acomodar la ecuación para obtener

Debe ser obvio que los valores de x que son soluciones a estas ecuaciones son  ± Öc.

Sea Xo una aproximación inicial a la solución de x = F(x) entonces se tomará como x = F(Xo)

Procediendo de esta  manera, la en-ésima aproximación, llamada también n-ésima iteración, es

La cuestión fundamental es: ¡Convergen los valores de Xn a la socucion correcta de x = F(x) conforme n crece?

Representación diagramática del método de aproximaciones sucesivas para 0 < f '(x) < 1.

Considerando la representación geométrica del proceso. Cuando tratamos de resolver x = F(x) estamos buscando la intersección de la curva y = f (x) (segundo miembro de la ecuación) y la línea y = x (primer miembro). Obsérvece la representación geométrica en la que la curva y = f(x) no está especificada. Sea x = a el valor de la abscisa del punto de intersección; entonces a es una raíz de la función, la cual naturalmente no conocemos de antemano. 

Raíces de Ecuaciones

La determinación de las raíces de las ecuaciones es uno de los problemas más antiguos de las matemáticas y se encuentra con frecuencia en la computadora moderna, ya que es necesario determinar raíces de ecuaciones con una gran variedad de aplicaciones.

Considérese la ecuación cuadrática simple

Decimos que:

Son raíces de esta ecuación porque, para estos valores de x, la ecuación cuadrática queda satisfecha. En el caso más general se nos da una función de x, F(x) y deseamos encontrar un valor de x para el que  F(X) = 0

La función F(x) puede ser algebraica o trascendente; generalmente suponemos que es diferenciable.

En la práctica, trataremos con funciones cuyas raíces no tienen una solución cerrada simple, como en el caso de la ecuación cuadrática. Entonces recurrimos a métodos de aproximación de las raíces los cuales involucran dos pasos fundamentales:

1.- Determinación de una raíz aproximada.

2.- Refinamiento de la aproximación hasta algún grado de precisión preestablecido.

Práctica: Valor Intermedio

En esta ocasión la práctica correspondiente a valor intermedio nos determinó un cierto número de iteraciones con respecto a una función, en el compilador usamos una estructura for para el ciclo de repeticiones de las sumas. La función determinada en clase fue la siguiente:

Aquí se presenta el código usado:

Resultados:

*

Como conclusión es importante mencionar que se dice que un proceso de iteración definido por:  es convergente para un Xo, si la sucesión Xo, X1,... correspondiente es convergente.

Teorema del valor intermedio

Dicho Teorema establece que, sea f una función derivable real que satisface las siguientes propiedades:

  * f es continua en el intervalo cerrado [a,b]

  * f es derivable en el intervalo abierto (a,b).

Es decir si f es una función diferenciable sobre el intervalo [a,b], entonces existe un número c entre a y b tal que:

  * f’( c ) =   f (b) – f (a)

                            b – a

o lo que equivale,

  * f (b) – f (a) = f ’ (c) (b – a)

Solución de ecuaciones por Iteración.

En las matemáticas de Ingeniería, frecuentemente podemos hallar soluciones de ecuaciones de la forma:

f(x) = 0,

es decir, números Xo tales que f(Xo) sea igual a cero; aquí f es una función dadas. Ejemplos son: 

todas pueden escribirse de la forma f(x) = 0. Las dos primeras son ecuaciones algebraicas porque la f correspondiente es un polinomio, y en este caso las soluciones se llaman también raíces de las ecuaciones. Las otras ecuaciones se llaman trascendentes porque contienen funciones trascendentes. Fórmulas que den los valores numéricos exactos de las soluciones sólo existirán en casos muy sencillos. En la mayoría de los casos, tienen que usarse métodos de aproximación, en particular métodos de iteración. 

Un método de iteración numérico es un método tal que se eligen un Xo arbitrario y se calcula una sucesión Xo, X1, X2,.. de manera recurrente a partir de una relación de la forma:

  

Donde g está definida en algún intervalo que contiene a Xo y el recorrido de g se encuentra en ese intervalo. De donde, se calculan sucesivamente: X1 = g(Xo), X2 = g(X1), X3 = g(X2),... 

En esta sección, tanto el dominio como el recorrido de g(x) estarán sobre la recta real, posteriormente y aumentando la complejidad de un problema podrían ser ambas variables vectoriales. 

Practica: Epsilon de la maquina

Después de revisar el experimento con la  calculadora CASIO, nuestra siguiente prueba fue en laboratorio con el compilador Dev C++.

En la máquina se procedió a programar con la ayuda de un ciclo For, en la que se utilizaba el mismo algoritmo que en el ejercicio pasado con la calculadora CASIO (Ver la entrada anterior). 

Para el ciclo For se limitó a 40 repeticiones, es decir: for (b=0; b<40; b++)

Aquí se muestra el código completo utilizado:

Ahora, al momento de correr el programa nos arroja el siguiente resultado en pantalla:

Podemos notar a simple vista, como es que se le fue sumando esa fracción a cada unidad, pero nuestro objetivo es el valor épsilon, ahora podemos ver que se encuentra en el número 18, es decir el algoritmo "1/Ans", se tuvo que repetir 18 veces para que pudiéramos encontrar el valor epsilon. Recordemos que en el caso de la calculadora CASIO para que sucediera lo anterior el número de repeticiones fue 31 veces.

¿Qué podemos concluir ahora? Pues bien, retomemos la definición que describimos anteriormente y hagamos notar que la existencia del valor épsilon de la máquina es una consecuencia de la precisión finita de la aritmética en coma flotante. 

¿Y que representa entonces este valor? pues representa la exactitud relativa de la aritmética de la computadora. Podemos concluir entonces que es superior al de la calculadora CASIO.

Práctica 1

Épsilon de la calculadora científica.

De manera experimental se verificó en una calculadora Casio Modelo: fx-991ES PLUS, el siguiente algoritmo:


e = [ (1/2)/2/2... /2 ]

En la calculadora el algoritmo fue:

e = [(1/2)/Ans/Ans... /Ans]

de la siguiente manera como se muestra: 

De tal manera que el número n de veces que se repite la división o cociente depende del modelo de calculadora, en este caso para la calculadora Casio: n = 31, es decir, repetiremos el cociente "Ans/2" 30 veces. Dado lo anterior nos arrojará un valor, el cuál corresponde al valor Épsilon de la máquina, como se observa en la siguiente imagen:

Lo anterior quedará demostrado al momento en el que a ese valor épsilon se sumará la cantidad 1 y éste nos arrojara "aparentemente" el mismo valor 1, como lo denotamos por la ecuación en la entrada anterior de "Errores y equivocaciones". Aquí se muestra como arrojará el resultado:

Errores y equivocaciones.

Dado que en los cálculos se trabaja con un número finito de dígitos y se llevan a cabo un número finito de pasos, los métodos del análisis numérico, son procesos finitos y un resultado numérico es un valor aproximado del resultado exacto (desconocido), excepto en los casos raros en los que la respuesta exacta es un número racional suficientemente sencillo y puede usarse un método numérico que dé la respuesta exacta. 

Si a* es un valor aproximado de una cantidad cuyo valor exacto es a, entonces la diferencia ɛ= a* - a se llama error absoluto de a* o, brevemente, error de a*. 

De aquí que:

a* = a + ɛ

¿Qué es el Epsilon de una computadora?

El épsilon (ɛ) de la máquina es el número x positivo más pequeño tal que 1 + x se puede representar de manera precisa en la máquina, es decir, el épsilon es el número decimal más pequeño que, sumado a 1, la computadora nos arroja un valor diferente de 1, con lo anterior nos referimos a que no es redondeado. Representa la exactitud relativa de la aritmética del computador. La existencia del épsilon de la máquina es una consecuencia de la precisión finita de la aritmética en coma flotante.

.

Introducción: Análisis Numérico

Nos referimos a métodos numéricos, como los procesos para obtener resultados numéricos a partir de ciertos datos dados. La rama de las matemáticas que se refiere al desarrollo de tales métodos se llama análisis numérico. 

El desarrollo del análisis numérico está fuertemente influido y determinado por la llegada y uso de la computadora, la cual en la actualidad es indispensable en el trabajo matemático de todo ingeniero. Este desarrollo incluye la creación de métodos nuevos, la modificación de métodos existentes para hacerlos más efectivos en el cálculo automático. En resumidas palabras un análisis teórico y práctico de los algoritmos para los procesos estándar de calculo y el señalamiento de aquellos algoritmos que son satisfactorios en diversas situaciones. 

Este curso es fundamental para todo ingeniero, puesto que implica una exploración o investigación de los algoritmos necesarios para llevar a cabo un proceso. El propósito de esta pequeña introducción es mostrar la punta del iceberg, posteriormente ahondaremos en el tema, con resultados prácticos vistos en laboratorio.